[알고리즘] [DP] 누적합(Prefix Sum)
1. 개념
1.1. 정의

누적합은 배열이나 리스트의 특정 구간의 합을 빠르게 계산하기 위해 사용되는 알고리즘 기법이다.
특정 구간의 합을 반복적으로 계산할 때, 한 번의 사전 계산으로 이후의 구간 합을 효율적으로 구할 수 있도록 돕는다.
1.2. 특징
전처리 단계
- 누적합을 구하는 배열을 생성하기 위해 처음에 한 번만 계산을 수행한다.
- 이 단계의 시간 복잡도는 일반적으로 선형 시간 O(n)이다. 단, 2차원 누적합 배열인 경우 2차 시간 O(n^2)이다.
빠른 구간 합 계산
- 이후 특정 구간의 합을 계산할 때, 누적합 배열을 통해 상수 기간 O(1)에 구간 합을 효율적으로 구할 수 있.
메모이제이션의 일종
- 이전에 계산된 값을 저장하여 이후 연산에 재사용하기 때문에, 동적 프로그래밍과 유사하게 중복된 계산을 줄여 성능을 향상시킨다. => 누적합은 곧 동적 프로그래밍(Dynamic Programming)의 일종이다.
cf) 동적 프로그래밍에 관한 포스팅은 추후에 할 예정이다.
2. 구현
본고에서는 Java를 사용하여 2차원 누적합 배열을 구현해보고자 한다.
2차원 누적합 배열은 2차원 배열의 구간 합을 계산할 수 있으며, 1차원 배열과 달리 상하좌우의 값을 함께 더하고 빼서 구간을 구성하는 방식이다.
2차원 배열의 누적합은 왜 상하좌우의 값을 같이 고려해야할까?
처음에는 2차원 배열의 누적합도 1차원 배열과 같이 직전 인덱스에 대한 누적값에 해당 인덱스의 값을 더하는 방식이라고 생각했었다.
그러나 이는 2차원 배열 누적합의 사용 목적을 제대로 파악하지 못했기 때문에 발생한 착각이었다.
2차원 배열 누적합은 특정 직사각형 구간의 합을 구하기 위해 주로 사용된다.
따라서 이전 인덱스만 고려한다면 이는 1차원 직선 구간의 합이 되어, 2차원 누적합의 활용 목적에 부합하지 않는다.
2차원 배열의 누적합을 구하는 예시는 하단의 이미지를 참고할 수 있다.

만약 (3,3) ~ (5,5) 구간 합을 구하고자 한다면,
1. sum[5][5] 의 값(전체의 구간 합)에서
2. sum[5][3] 의 값(노란색 영역)을 빼고
3. sum[2][5] 의 값(초록색 영역)을 뺀 뒤
4. 중복 제거한 sum[2][2]의 값(노란색과 초록색이 겹치는 영역)을 한 번 더해준다.
이를 코드로 구현하면 다음과 같다.(https://www.acmicpc.net/problem/11660 참고)
package SSG_coding_test.week1;
import java.io.*;
public class BOJ11660 {
/*
* 구간 합 구하기 5
* (x1, y1) ~ (x2,y2) 합 구하기
*
* => 1. 이차원 배열 3중 반복문 ==> 연산횟수 1억번 넘어감 => 시간초과
* => 2. 일차원 배열로 변환 => O(N^2 * M) => 연산 횟수 1억번 이상
* => 3. 누적합
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 1. N, M 입력 받기
String[] input = br.readLine().split(" ");
int N = Integer.parseInt(input[0]);
int M = Integer.parseInt(input[1]);
// 2. 표 입력 받기
int[][] table = new int[N+1][N+1];
for (int i = 1; i <= N; i++) {
String[] line = br.readLine().split(" ");
for (int j = 1; j <= N; j++) {
table[i][j] = Integer.parseInt(line[j - 1]);
}
}
// 3. 누적합 배열 생성
int[][] sum = new int[N+1][N+1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
sum[i][j] = table[i][j] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1];
};
}
// 3. x1, y1, x2, y2 입력 받기
int[][] xy = new int[M][4]; // x : 행 / y : 열
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
String[] line = br.readLine().split(" ");
int x1 = Integer.parseInt(line[0]);
int y1 = Integer.parseInt(line[1]);
int x2 = Integer.parseInt(line[2]);
int y2 = Integer.parseInt(line[3]);
int result = 0;
if(y1 == 0){
result = sum[x2][y2] - sum[x1-1][y2];
} else {
result = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1];
}
sb.append(result).append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
}
3. 활용
3.1. 활용 사례
누적합 알고리즘은 반복적으로 구간 합을 계산하거나, 연속된 데이터의 합산 결과를 빠르게 구해야 하는 다양한 분야에서 사용된다.
3.1.1. 데이터 분석
시계열 데이터( 時系列 data; Time-series data)
- 시간 순서에 따라 관측된 데이터를 의미한다.
- 누적합은 시계열 데이터에서 추세를 파악하기 위해 일장 기간 동안의 평균, 최댓값, 최솟값 등을 구하는 데 활용된다.
- 하단의 주가 그래프가 대표적인 시계열 데이터이다.
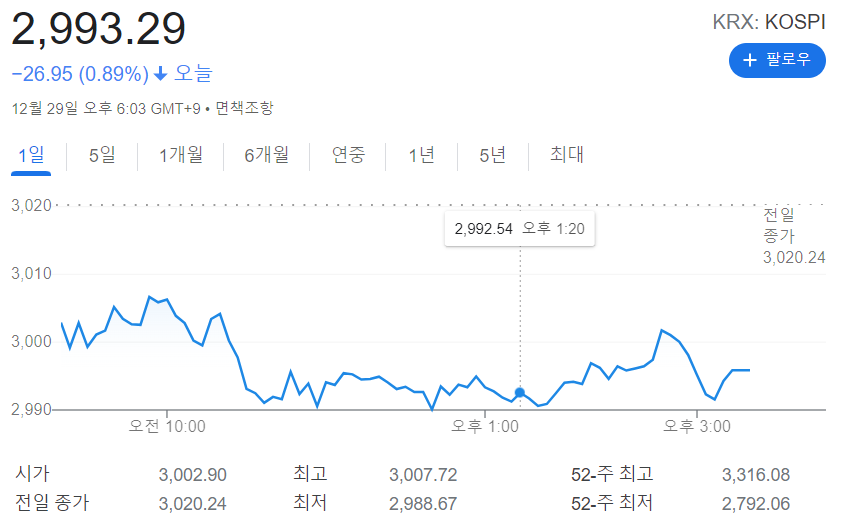
웹 로그 분석
- 일일 방문자 수, 페이지뷰 데이터 등을 누적합으로 처리하여 특정 기간의 트래픽을 빠르게 조회 가능하다.
재고 관리
- 제품별 일일 출고량을 누적합으로 관리하면 특정 기간의 출고량을 빠르게 계산 가능하다.
3.1.2. 컴퓨터 그래픽스 및 이미지 처리
합산 영역 테이블(Summed-Area Table; 적분 이미지, 적분 영상)
- 이미지 내에서 특정 구간의 밝기 합을 빠르게 계산하는 기법이다.
- 예컨대, 사진의 특정 영역에서 픽셀 값을 빠르게 추출하거나 특정 구간의 색상 값의 평균을 계산할 때 누적합 배열을 사용해 성능을 향상시킨다.
3.2. 코딩테스트 등장 유형
누적합 알고리즘은 코딩 테스트에서 구간 합을 구하는 문제에 매우 효과적인 알고리즘이다.
3.2.1. 배열의 구간 합 문제
1차원 배열 혹은 2차원 배열의 특정 직사각형 구간의 합을 빠르게 계산하는 문제에서 사용된다.
3.2.2. 슬라이딩 윈도우와 결합된 문제
슬라이딩 윈도우 기법과 결합해 일정 범위의 합을 구하고, 윈도우 이동 시 구간 합을 빠르게 갱신하는 방식으로 사용된다.
예컨대, 고정된 길이의 연속된 구간에서 최대합을 찾는 문제에서 슬라이딩 윈도우와 누적합을 결합해 최적화할 수 있다.
3.2.4. 부분합 및 부분적 조건 만족 문제
배열에서 특정 조건을 만족하는 부분 합의 길이, 또는 특정 구간 합이 목표치에 도달하는 최단 거리 문제 등에서 사용된다.
예컨대, 특정 구간에서 합이 일정 값 이상이 되는 최소 구간 길이를 구하는 문제에서는 부분합과 누적합을 함께 사용 가능하다.